Stuart Haber and W. Scott Stornetta’s paper, “Secure Names for Bit-Strings,” Proceedings of the 4th ACM Conference on Computer and Communications Security (1997: 28-35), is a second essay cited by Satoshi Nakamoto in the Bitcoin whitepaper. They build on a feature of their earlier ‘91 essay, “How to Time-Stamp Digital Documents”. In addition, “Secure Names for Bit-Strings” offers a naming scheme using Merkle trees; Ralph Merkle is in the acknowledgments and they are explicit about it in section 2.4. Merkle trees have become widely adopted in the blockchain space and so this is another connection to the present, albeit applied to naming bit-strings in digital documents.
Two desirable features of a digital document are that it satisfies a useful naming scheme for retrievability - that they can be easily found - and that the integrity of the document can be verified. The second feature is the focus of this paper: “how to make sure that the bit-string content of a given digital document is indeed the same as the bit-string that was intended.” Before diving into their proposed scheme, I’ll first comment on what bit-strings are.
A bit-string is a sequence of bits, an ordering of 0’s and 1’s: ‘01100010’. It is the machine-friendly version of the content that makes up the digital document. Haber and Stornetta do not go into detail about what a bit-string is, leaving open whether it includes metadata. To avoid discussions of what is data vs metadata, for simplicity, think of the bit-string as containing the content that is to be protected and not subject to tampering.
Some early requirements for an acceptable solution for an integrity mechanism:
- It should not require burdensome infrastructure, such as required for digital signatures
- It should not depend on the secrecy of a cryptographic key
One-way hash functions are one way to go, but they have challenges too:
- The resultant name must be long-lasting, not easily requiring an update due to technological advances.
- The hash values should not be too long.
- One-way hash values usually appear random, as if removing control over the form of the name from the author.
Haber and Stornetta propose a “method for naming bit-strings that retains the verifiable security of hash-based names, while avoiding constraints listed above, as well as avoiding the use of secret cryptographic keys…. the essence of the new scheme is to keep a repository of hash values that depend on many bit-string inputs, and to name each bit-string by a concise description of a location in the repository to which it can be securely ‘linked’ by a one-way hashing computation.” (p. 29)
Preliminaries
Haber and Stornetta go into more detail on the nature of the problem in this section. There have been previously built naming systems to satisfy retrievability and having confidence that one has the right document, e.g., URNs. But previous systems depend on either the digital signature or one-way hash functions. The authors spend more time on the challenges here before proposing their own solution. To be clear: their solution does not denounce these as illegitimate tools; see the next section.
Hash functions
The principal technical tool we use in this paper is that of a one-way hash function. This is a function compressing digital documents of arbitrary length to bit-strings of a fixed length, for which it is computationally infeasible to find two different documents that are mapped by the function to the same hash value. (Such a pair is called a collision for the hash function.(p. 29)
The authors here give a formal definition of a family of collision-free hash functions taken from Ivan Damgård (1988). He defined a family of collision-free hash functions to be a family $\{H_k\}_k$, for which k is a security parameter. In other words, there is a family of hash functions where k is the fixed length of their output bits (that is the part on the inside of the brackets); the security of these hash functions, e.g., against finding collisions, scales up as the size of k increases.
Three properties of these collision-free hash functions are given.
-
Any length of bits, $\{{0, 1}\}^*$, that can be mapped to some bit-string of a fixed length, $\{{0, 1}\}^k$, can be computed quickly (e.g., polynomial time).
-
Given k, the security parameter (a configurable value), it is easy to choose a hash function from the set $H{_k}$.
-
It is computationally infeasible, given a random choice of the functions in the family, to find a collision for the function. There is a more precise definition. The $\Pr[h \leftarrow H_k; (x, x’) \leftarrow A(h): x \neq x’, h(x) = h(x’)] < k^{-c}$ holds for any polynomial-time algorithm $A$ and constant $c > 0$, as $k$ becomes sufficiently large.
The probability of computational infeasibilty in property 3 works like this: you randomly pick $h$ from $H_k$, and let algorithm $A$ try to find different $x$ and $x'$ where $h(x) = h(x’)$. The chance $A$ succeeds is less than $1/k^c$, where $c$ is any positive number. As $k$ (the security parameter) gets bigger—say from 64 to 256—the odds drop sharply, like $1/64^c$ to $1/256^c$. This means no fast algorithm can reliably find a collision, making the family secure as $k$ scales up.
Although Damgård gave a proof of the existence of such functions, Haber and Stornetta say they are infeasible because computers will get faster. They cite Dobbertin’s attacks on MD4 and MD5 as an example. Once hardware catches up, the hashes of yesterday could be broken.
Theoretical Model
The authors present an abstract model of the problem: what a naming scheme is, what an counterfeiting adversary is, and what makes a naming scheme secure. They illustrate these using a server S and a repository R, but these are not required.
A naming scheme consists of:
- Security parameter k;
- A polynomial-time naming protocol N taking as input a bit-string x and outputs a name n for x and a certificate c, and adds items to the repository R;
- A polynomial-time verification protocol V that takes as input the triple (x, n, c) and the result query to R, then either accepts or rejects.
Cooking up a fake certificate is not likely to work because the validation protocol checks the certificate and name with the data stored in the repository. The naming protocol outputs (n, c) and adds at least the pair (n, x) (or a hash of x and related data) to R. The repository is queried during validation to retrieve this stored information, ensuring consistency and preventing forgery.
A counterfeiting adversary is a polynomial-time algorithm (possibly probabilistic) that, given the security parameter k, generates a sequence of bitstrings $x{_1}$ to $x{_t}$ and observes the outputs of the naming protocol N on each. It can also query the repository R any polynomial number of times. Its goal is to output a new triple (x, n, c) where x was never input to N, yet the validation protocol V accepts it based on R’s state — that is, forging a verifiable name without using N.
A naming scheme is secure if, for any such adversary, the probability of successful counterfeiting is less than $k^{-c}$ for any constant c and sufficiently large k (i.e., negligible in k). That is, the larger k, the less likely an adversary would be successful. The odds of success drop faster than any polynomial; their odds shrink not to zero, but are practically indistinguishable from zero.
These are definitions. There is no proof to be given.
Digital time-stamping
The authors apply their abstract model to their 1991 work on digital time-stamps by using Merkle trees. This is a concrete implementation of the definitions earlier, though a single attack vector remains. They make an application with digital time-stamps to prepare the next section where they apply the strategy to names.
In this scheme, a coordinating server collects hash values of documents submitted during a fixed interval, arranges them as leaves in a binary Merkle tree, and computes a single root hash that represents the entire batch. This root is then hashed together with the previous interval’s root and published in a widely available repository, forming a chain over time. Each requester receives a certificate consisting of the interval’s end time and the sequence of sibling hashes needed to reconstruct the root from their own leaf. Verification requires only the public root from the repository and local recomputation along the path; the mathematics guarantees that no document can be altered or backdated without breaking the hash chain.
The only remaining vulnerability is the integrity of the repository itself: if an adversary replaces a published interval hash, all certificates from that interval become untrustworthy. By reducing trust to this single, public, append-only data structure, the scheme eliminates reliance on secret keys or honest servers after issuance.
The naming scheme for bit-strings
The main point of this section is that one can create a chain of hashes where each link proves the existence and integrity of every bit-string before it, publicly, via cryptographic linkage.
There is a server S acting as the coordinating server. S announces that it has randomly chosen h as the one-way hash function from the family of hash functions. S will compute certificates in response to requests for secure names and make additions to the repository R.
The significance of the chosen hash being announced is that the server cannot change hashes between user requests. That would make it impossible to verify the results. By announcing the hash function h from the family of $H{_k}$, we do not have to trust S to behave honestly during verification: the public commitment binds S to a single, fixed h for all participants. Anyone can independently recompute the Merkle path and chain using the announced h and the public repository R — if S deviates, the math fails, and the forgery is detected without needing to trust S at all.
The main move appears when they write,
We abbreviate a bit-string’s certificate by omitting the list of hash values, leaving only a pointer to the relevant interval hash… and an encoding of the position of the request in the tree for that interval. It is this abbreviation that we propose to use as the name of the bit-string. (p. 31)
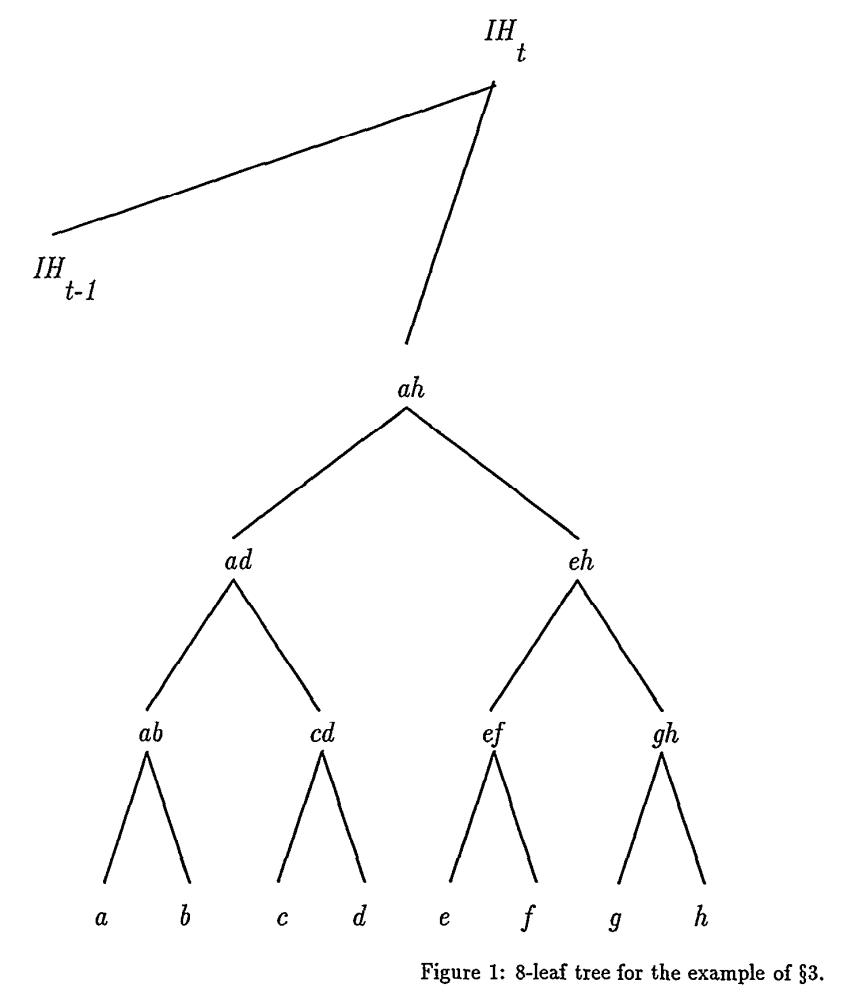
What they are saying is that the secure name consists of the position in a chain (e.g., by a pointer) and an encoding of the position of the request in that interval in the tree. There are two parts to a secure name. The “interval” refers to a time-bounded batch of requests (common in timestamping systems), and the pointer t indexes a specific chain position or timestamp. Recall as well that the requests are leaves in the Merkle tree. Then it would make sense to think of the encoding as having a collection of branches. And that’s why they list b in the second part: n = (t; $b{_1}$,…,$b{_l}$). They are turning a long certificate into a short name by dropping the heavy hash list and keeping two things - where it occurs and the branch choices.
The encoding tells the exact branch by branch position of the request for each level. In the example for the request at leaf c, they give:
- (d,R),(ab,L),(eh,R),($IH_{t-1}$,L)
We know that in the tree c has d as the right sibling. Up one level is cd, which has ab as its sibling to the left. With their diagram it is easier to see this now:
On this scheme, the security reduces to one thing: collision resistance of the hash function.
Security
The security boils down to this theorem:
Theorem 1
If ${H_k}_k$ is a family of collision-free hash functions, then the naming scheme [N, V, S] described above is secure.
The server S starts by choosing a single hash function h from the family $\{H_k\}_k$. This choice is publicly announced to everyone. From this point forward, every hash in the system uses this exact same h. The security parameter k controls how hard it is to find two different inputs that produce the same hash output. A collision means finding two different bit-strings x and y such that h(x) = h(y).
Suppose an adversary tries to forge a name. That is, the adversary wants to make a fake bit-string x’ (which was never submitted to S) appear to have a valid name. To do this, he must produce a name n and a certificate c such that the validation protocol V accepts them when querying the repository R.
The authors show that this is only possible if the attacker can create a hash collision under the announced h.
They argue:
if x is a bit-string on which N was never invoked during a run, any triple (x, n, c) that V will accept (after the correct response to a query to R) will include a hash collision for the function h announced by S at the beginning of the run: either x itself or one of the hash values $z_i$ in c (when combined on the left or the right with $y_i$) collides with another argument to h whose hash value was computed during the run. (p. 31, section 3.1)
In other words, the attacker must make fake data produce the same hash as real data — either at the leaf or along the path. But since h is fixed, public, and collision-resistant, no such fake is possible. Thus, no counterfeit can succeed.
The authors are clear that the security of the naming scheme does not depend their specific data structure chosen (e.g., a binary tree). In their words now, the security is due to “making portions of the graph widely witnessed and widely available. To insure the verifiability of the names, it suffices that every document in the naming structure be linked by a directed path to a widely witnessed hash value; a standard ordering of the incoming edges at each node can be used to encode the path. Then the name of a document is given by this encoding of its location in the graph, together with a pointer to the hash value at the end of the path, and the argument of Theorem 1 applies.” (p. 31, section 3.2)
Applications and more
The core of the paper has been presented in the first three sections described above. The remaining sections show how to apply this, e.g., to URLs (Section 4); how names can be long-lived and renewed (Section 5); there are variations like swapping out their encoding section in the name for, say, a MIME encoding of unix time (Section 6).